Illustrating Metaphysics

Jack S. Crumley II’s new book, An Introduction to Metaphysics features original illustrations by Guelph, Ontario artist, Gillian Wilson, alongside the text. These illustrations are meant to both instruct and delight: they help to reinforce the central ideas in each chapter and entertain the reader. Below are some samples of the illustrations along with their corresponding passages from the book.

From Chapter 5: Things

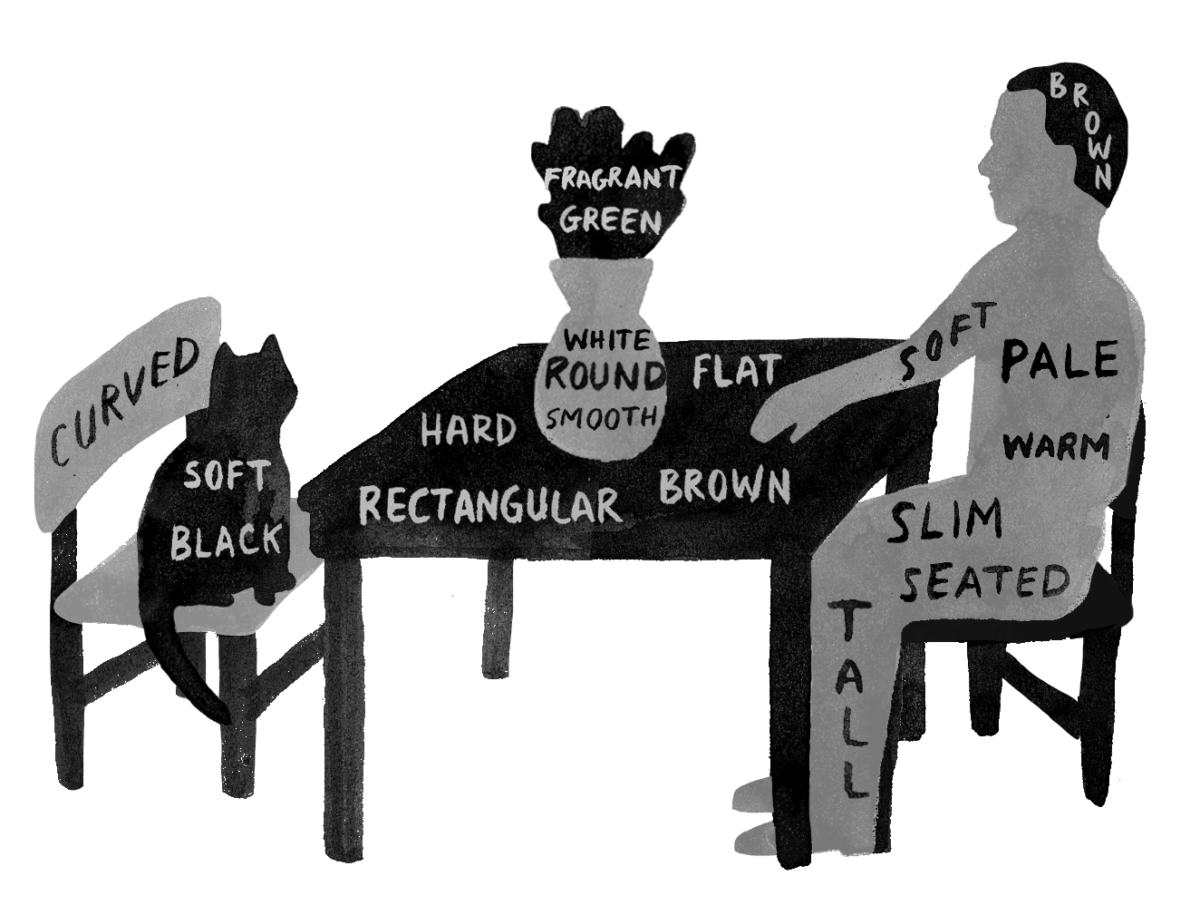
Berkeley’s skepticism about material substance and Hume’s skepticism about the notion of substance in general led them to a view, still held by many in one form or another, known as the bundle theory—the view that objects are nothing more than collections, or “co-locations” of qualities. There is no substance, no essence; nor is there any property-less substratum that holds together or supports an object’s qualities. For example, two candles sit in front of me. Each cylindrical, each six inches high and three inches in diameter. But one is red and the other green. The qualities constitute or make up the candles. That’s all there is to these two candles. A certain, shape, height, weight, scent, color. And what is true of the candles is true of every object, animate or inanimate.

But wait—if things are only their qualities, and nothing but their qualities, there is a surprising consequence: any change of quality changes the identity of the object. An apparent advantage of the substance view is that it explains how an object changes but remains the same object. Yet, according to bundle theory, if Julia paints the bookcase red, we have a different object from the white bookcase we had before!

From Chapter 7: Personal Identity

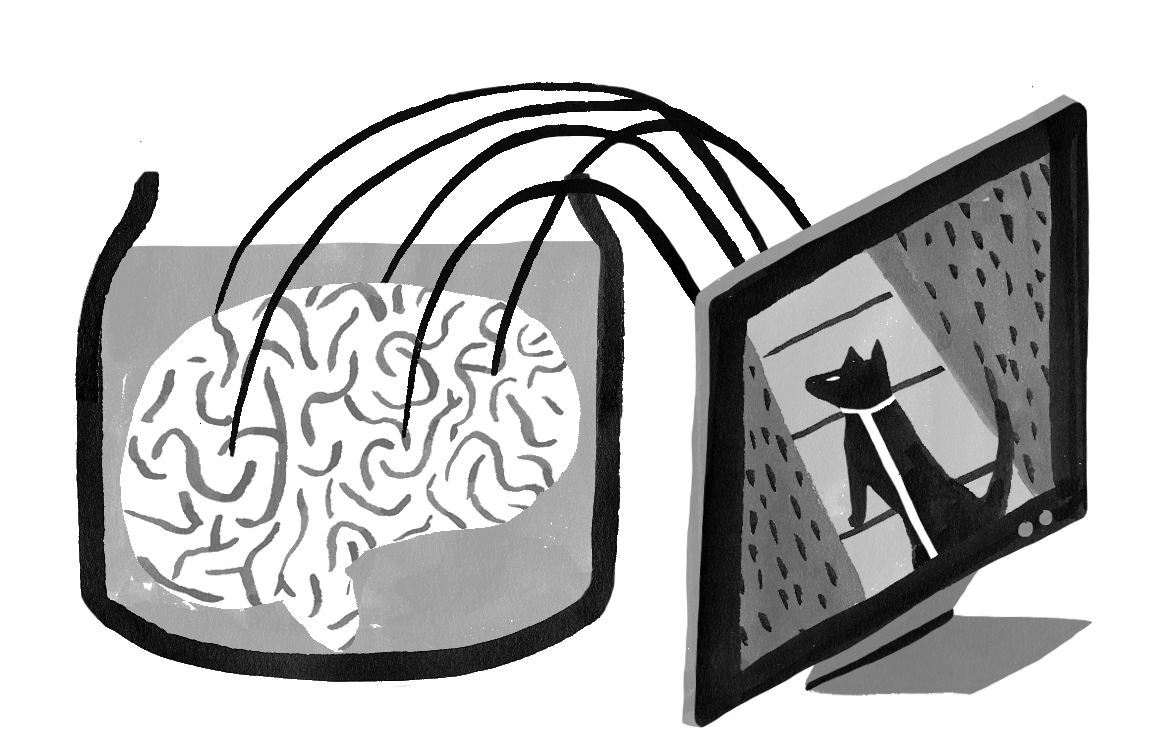
Can we imagine losing parts—even significant parts—of the body, yet still being ourselves? Not only might we lose a limb or an eye, imagine losing the whole body, except for the brain. If we could find a way to preserve the brain—to allow it to continue functioning—then we might think that our identity is still preserved. Recent philosophy sometimes describes this preservation sans body as a “brain in a vat.” As long as our brains continue functioning, we continue. Our identity therefore is determined by or constituted by a functioning brain: persons remain the same over time, if their brains continue. Deirdre is the same person today as she was yesterday if she has the same brain she had yesterday. And here we can understand “same brain” in like manner as we understood “same body.”

From Chapter 9: Time

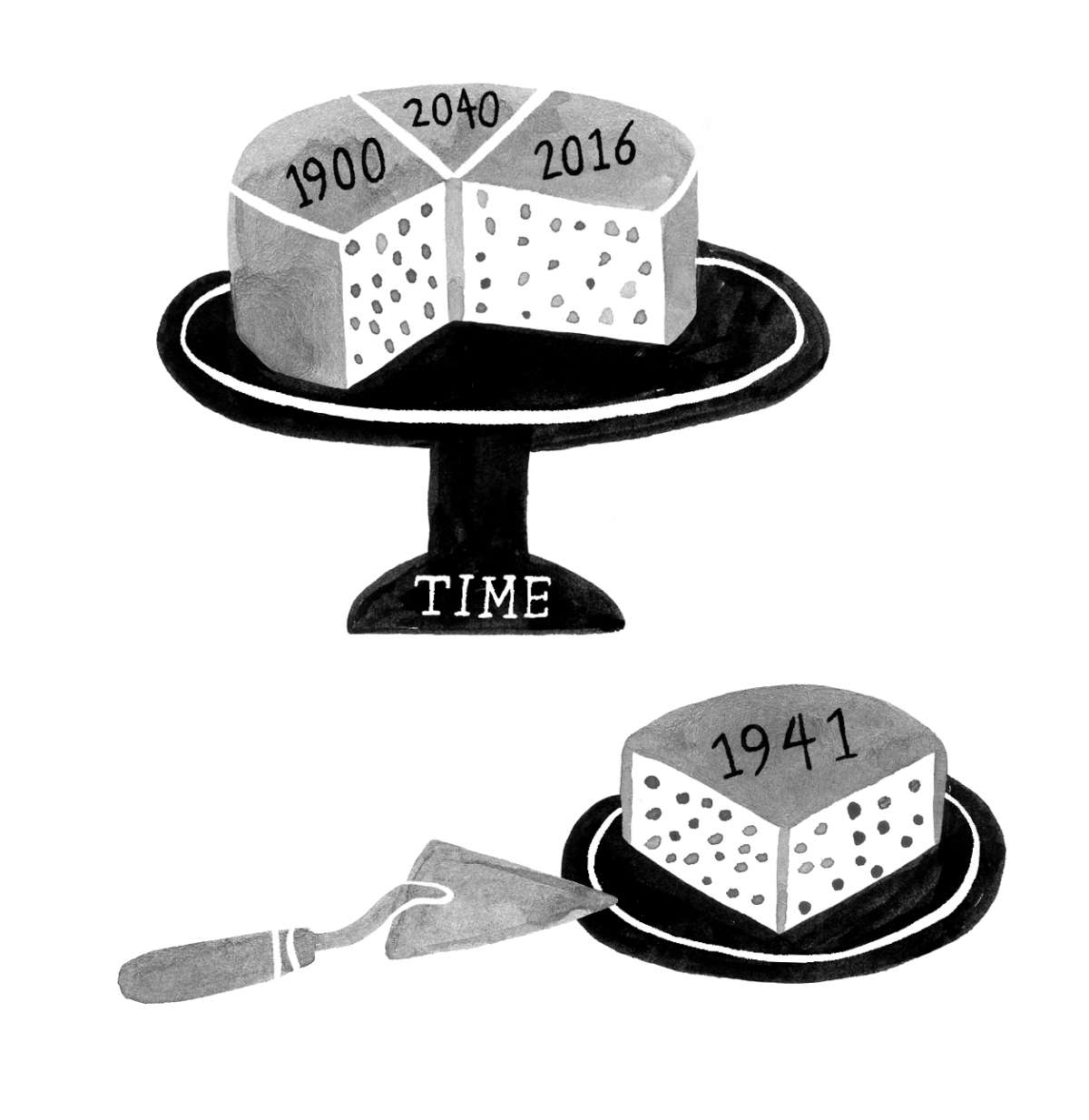
All times exist equally. If this is correct, then there is no reason to see the essential nature of time as a sequence of moments, directed from 1941 to 2016. There is thus no ontological priority of an event that we identify as being earlier than some other event. Although our ordinary conversations might do so, we shouldn’t assume that those conversations reflect the nature of reality. Given this picture of the reversibility or symmetry of time, backwards causation may be infrequent, but it is metaphysically possible.

From Chapter 11: Why Is There Something Rather Than Nothing?

Numbers are sometimes considered as sets, but they are also thought of by some as universals. Fortunately, that issue need not be settled here. Yet numbers are abstract objects. At a very early age, I was taught that I could demolish all the instances of the numeral two (an inscription of some sort that “referred to” the number), but I would not for all my effort have done anything to alter the number two. This is simply to reinforce the idea that numbers are not physical (spatio-temporal) objects, but abstract objects.